Intro to SVM (Support Vector Machine)

A Support Vector Machine (SVM) can be imagined as a surface that defines a boundary between various points of data which represent examples plotted in multidimensional space according to their feature values. The goal of an SVM is to create a flat boundary, called a hyperplane, which leads to fairly homogeneous partitions of data on either side. SVMs can be adapted for use with nearly any type of learning task, including both classification and numeric prediction. Many of the algorithm’s key successes have come in pattern recognition. Notable applications include:

• Classification of microarray gene expression data in the field of bioinformatics to identify cancer or other genetic diseases
• Text categorization, such as identification of the language used in a document or organizing documents by subject matter
• The detection of rare yet important events like combustion engine failure, security breaches, or earthquakes

SVMs are most easily understood when used for binary classification, which is how the method has been traditionally applied.

Classification with hyperplanes

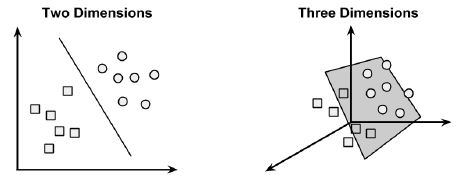
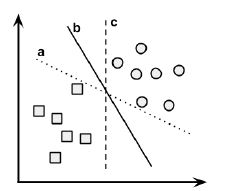
SVMs use a linear boundary called a hyperplane to partition data into groups of similar elements, typically as indicated by the class values. For example, the following figure depicts a hyperplane that separates groups of circles and squares in two and three dimensions. Because the circles and squares can be divided by the straight line or flat surface, they are said to be linearly separable. The task of the SVM algorithm is to identify a line that separates the two classes. As shown in the following figure, there is more than one choice of dividing line between the groups of circles and squares. Three such possibilities are labeled a, b, and c.

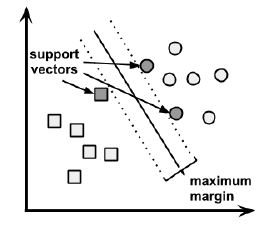
Finding the maximum margin

The answer to that question involves a search for the Maximum Margin Hyperplane (MMH) that creates the greatest separation between the two classes. Although any of the three lines separating the circles and squares would correctly classify all the data points, it is likely that the line that leads to the greatest separation will generalize the best to future data. This is because slight variations in the positions of the points near the boundary might cause one of them to fall over the line by chance. The support vectors (indicated by arrows in the figure that follows) are the points from each class that are the closest to the MMH; each class must have at least one support vector, but it is possible to have more than one. Using the support vectors alone, it is possible to define the MMH. This is a key feature of SVMs; the support vectors provide a very compact way to store a classification model, even if the number of features is extremely large.

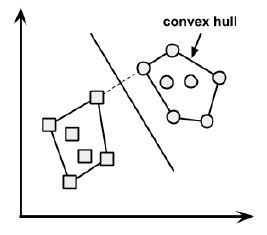
The case of linearly separable data

It is easiest to understand how to find the maximum margin under the assumption that the classes are linearly separable. In this case, the MMH is as far away as possible from the outer boundaries of the two groups of data points. These outer boundaries are known as the convex hull. The MMH is then the perpendicular bisector of the shortest line between the two convex hulls. Sophisticated computer algorithms that use a technique known as quadratic optimization are capable of finding the maximum margin in this way. To understand this search process, we’ll need to define exactly what we mean by a hyperplane. In n-dimensional space, the following equation is used: